Initiation à la programmation en python


Pour créer une liste vide appelée positions on écrit : positions = []
Directement, on peut écrire positions = [10, 20, 30]
On obtient alors : positions[0] = 10 ; positions[1] = 20 et positions[2] = 30
Piège : positions[3] n’existe pas !
Pour ajouter le nombre 50 à la fin de la liste positions, on écrit : positions.append(50)
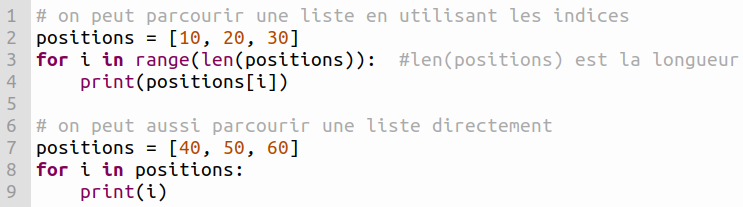
Voici les deux méthodes pour parcourir une liste qui s’appelle positions :
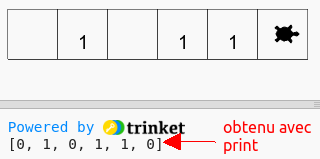
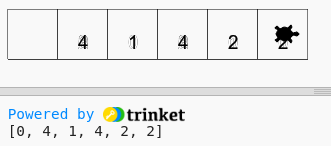
Le robot parcourt le couloir puis affiche (à l’aide de la commande print) une liste qui donne les emplacements des billes
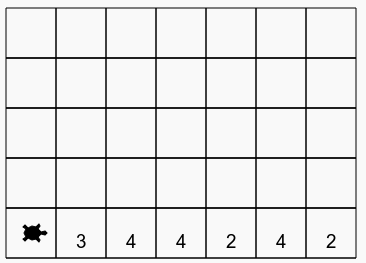
Chaque case a 1 ou 0 bille, la taille du couloir est inconnue



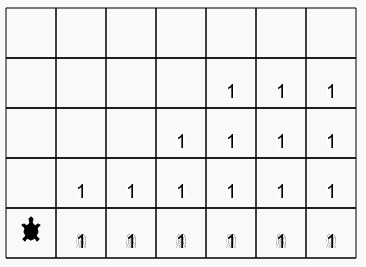
On reprend presque l’exercice 1, mais cette fois les cases du couloir peuvent posséder plusieurs billes

 version en ligne
version en ligne
Pour cet exercice on parcourt une liste qui s’appelle positions et qui est donnée dès le début
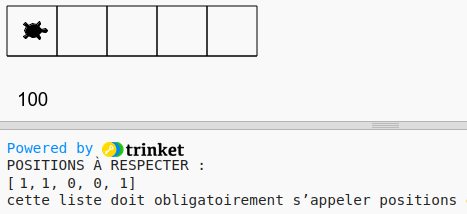
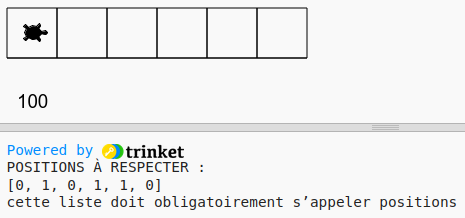
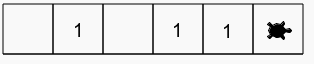
On fait l’exercice 1 à l’envers : une liste positions est donnée, il faut remplir le couloir qui lui correspond
Vous avez l’obligation d’appeler positions la liste qui donne les emplacements
Heureusement, le couloir qui apparait possède le bon nombre de cases… il ne reste qu’à le remplir

Le couloir est à moitié rempli de billes (sans aucune case vide), l’autre moitié est vide.
Le robot parcourt le couloir et décale sur la seconde moitié les billes
(afin de rendre l’exercice infaisable sans les listes il suffit d’interdire au robot de faire marche arrière, c’est à dire ne lui autoriser que de se déplacer de gauche à droite)


Le couloir est à moitié rempli de billes (sans aucune case vide), l’autre moitié est vide.
On reprend presque l’exercice 4 :
Le robot parcourt le couloir et décale de façon symétrique sur la seconde moitié les billes
(là encore on interdit au robot de faire marche arrière)


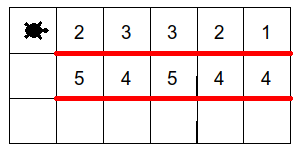
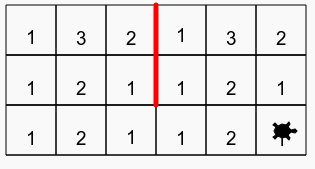
Le couloir a 3 étages : les deux premiers avec des billes, le troisième est vide
Le robot doit faire la somme des deux premières lignes et écrire le résultat sur la 3ième ligne :
chaque case de la troisième ligne est la somme des deux cases au dessus d’elle
(la somme ne dépasse jamais 9)
Les lignes rouges sont infranchissables (il faut donc bien utiliser une ou des listes)

Cet exercice particulièrement difficile demande de connaître le triangle de Pascal
(notion vue en Terminale spé mathématiques)
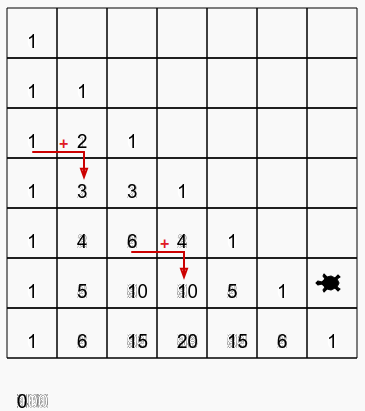
Pour que l’exercice soit intéressant il faut s’interdire d’utiliser les coefficients binomiaux (et donc les factorielles) et tout faire par récurrence comme le montre le dessin ci-dessous (les élèves de Terminale spé maths comprendront la consigne…)
Si vous n’êtes pas particulièrement fortiche, passez votre chemin !
Le robot doit faire apparaître le triangle de Pascal jusqu’à n = 6


On reprend l’exercice 3 mais en plus difficile : nous ne sommes plus dans un couloir mais dans une pièce
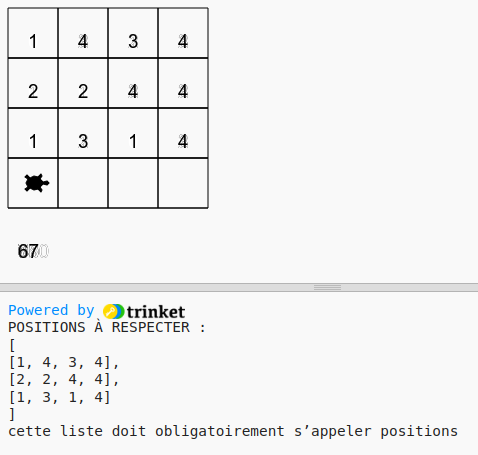
Une liste positions est donnée, il faut remplir la pièce qui lui correspond
La liste positions est elle même constituée de listes qui représent les lignes à obtenir
Vous avez l’obligation d’appeler positions la liste qui donne les emplacements
Ci-dessous la liste [ [1, 4, 3, 4] , [2, 2, 4, 4] , [1, 3, 1, 4] ] est représentée avec des retours à la ligne
(c’est tout à fait autorisé en python et souvent utilisé pour plus de lisibilité)

Le robot doit reproduire à l’identique la répartition des billes dans la deuxième salle
(on va pas se mentir : la moitié du programme correspond à l’exercice 8)
Les dimensions des salles et la répartition des billes sont aléatoires
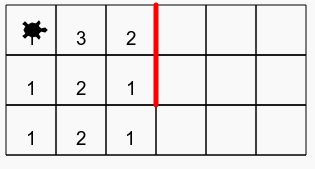
On reprend l’exercice 6 de la page while
Mair cette fois-ci il faut étaler les billes verticalement du plus petit au plus grand !
Eh oui, encore un exercice particulièrement difficile car il faudra trier une liste du plus petit au plus grand élément
(à moins de tricher : pour trier une liste L, il suffit d’écrire L.sort() , mais l’exercice perd de son intérêt)