Initiation à la programmation en python
Pour créer une variable entière x égale à 0 on écrit x = 0
Pour augmenter la variable x de 1 on écrit x = x + 1
On s'efforce de donner des noms compréhensibles aux variables
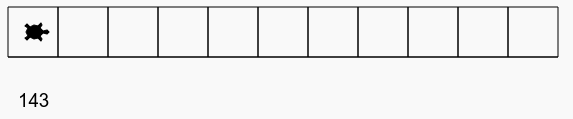
Le robot est dans un couloir.
A la fin il annonce la taille du couloir.
Le robot est dans un couloir, certaines cases sont vides, d'autres avec des billes.
A la fin le robot annonce le nombre de cases vides.
Le robot est dans un couloir dans lequel il y a des billes.
A la fin il annonce le nombre total de billes dans le couloir.
Le robot est dans un couloir dans lequel il y a des paquets de billes.
A la fin chaque paquet de billes a deux fois plus de billes.
(on suppose que le robot commence sur une case vide et qu'il a suffisamment de billes au début pour être sur
de ne pas en manquer)
Le robot est dans un couloir avec 45 billes dans sa poche.
Il dépose une bille sur la première case, deux sur la deuxième et ainsi de suite.
On reprend l'exercice précédent mais on ne sait pas combien le robot a de billes en poche.
Il dépose une bille sur la première case, deux sur la deuxième et ainsi de suite.
Lorsqu'il n'a plus assez de billes pour remplir correctement une case il s'arrète.
Cet exercice est particulièrement important !Le robot est dans un couloir dans lequel il y a des tas billes.
A la fin il annonce la taille du plus gros tas de billes.
Le robot est dans un couloir dans lequel il y a des tas de billes sauf sur la dernière case.
Il décale les tas de billes d'une case.
Le robot a 70 billes en poche et les dispose comme le montre la figure ci-dessous
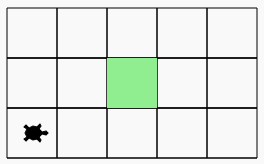
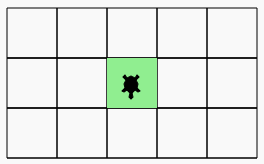
Le robot doit finir sur la case colorée (c’est la case au centre de la pièce rectangulaire)
La pièce change de dimension à chaque fois,
mais il y a toujours un nombre impair de cases en largeur et en longueur
Le robot doit écrire les 10 premiers termes de la suite de Fibonacci
Ce qui signifie que chaque case comporte autant de billes que les deux précédentes
(avec les deux premières cases qui comportent 1 bille chacune)
À écrire en une dizaine de lignes seulement !
